A few days ago, while I was trying to optimize the rendering code of a designer application I found something funny about Java 2D, there is no easy way to check if a rectangle intersects with a QuadCurve2D. That is with just the curve, not the area enclosed by it. I’ll try to summarize what I learned about quadratic bezier curves, and provide a fast algorithm to check for the intersection.

Quadratic bezier curves are defined by three points: a starting point, a control point, and an end point. The starting point and the end point are on the curve, the control point is outside the curve.

Bezier curves are based on the parametric equation of the line, which is of the form:

\[L(t) = P_1 (1 - t) + P_2 t\]

With \(t\) in \([0,1]\). \(P_1\) and \(P_2\) are two arbitrary points.

As I said before, a bezier curve is defined by three points. Take a look at the following diagram:

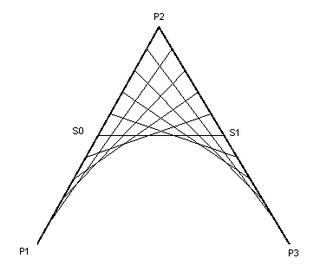
How a bezier curve is constructed

Here we have two main lines: from \(P_1\) to \(P_2\) and from \(P_2\) to \(P_3\), the curve is defined by a point in the line \(S_0\) to \(S_1\). Using the parametric equation of the line I mentioned before, we can write \(S_0\) and \(S_1\) as:

\[S_0(t) = P_1(1-t) + P_2 t\] \[S_1(t) = P_2 (1-t) + P_3 t\]

Then, the point on the bezier curve is defined as:

\[Q(t) = S_0(1-t) + S_1 t\]

Simplifying this (hocus phocus… and some mathematical mumbo jumbo) we get:

\[Q(t) = P_1 (1 - t)^2 + P_2 (2t(1-t)) + P_3 (t^2)\]

So finally we have the basic equation for a quadratic bezier curve.

(Next Curve Intersection)