NOTE: This is a revised version of an article I wrote for Medallia’s engineering blog

Sorting and paging is a very common problem. The gist of it is that you have a large amount of data that you filter and sort and for rendering purposes, you want a fixed size window into the sorted and filtered data.

There are two ways to model apis to request a page:

• use a reference element (call it r) and a pageSize, so you request a page of size pageSize, with elements after r
• use a pageStartIdx into the sorted data and a pageSize

The first case is relatively easy to distribute, and is the kind of strategy (with variations) that most sane large scale applications use. This first scenario is usually sharded by having each shard accumulate only values after r in pageSize sized priority queues, and then sending each to a coordinator node so they’re merged and any extra data is discarded (there are optimizations where you can build a tree of aggregations to reduce total traffic and distribute merging somewhat if you have many nodes).

The second scenario (using an offset and a page size) is much more interesting in my opinion and there’s little to none literature on how to solve it efficiently. This is the one is the one we will tackle in this article.

If you’re starting from scratch, do yourself a favor and pick the first strategy, it will save you countless headaches down the road, even if scale is not an issue yet. If on the other hand, you’re stuck with option two, keep reading.

Doing it the hard way

In the restricted case of an offset/page sort, all page offsets are page size aligned, that is:

pageStartIdx % pageSize == 0

I’ll focus on the general case, where you want a fixed size page starting at an arbitrary offset into sorted data, if we have:

• k: an offset into the sorted data as if it were in one place (i.e. as if it were large array)
• pageSize: desired page size

Let’s use an example, if the data were in one place (e.g. an array), and you want to go to offset 4 (k=4), with a page size of 3 (pageSize=3), it’s enough to just slice the sorted array:

Or in pseudo-code:

copyOfRange(data, k, min(k + pageSize, length(data)))

The function returns a new array and it has the following signature:

copyOfRange(int[] array, int fromInclusive, int toExclusive)

But what happens when your data is distributed?

Picture the situation when your data is spread on a number of shards, these shards are somewhat evenly sized and the data is randomly distributed among them (it’s not strictly required, but it helps and is usually somewhat close to reality).

The simplest approach is to have all shards send all data to a coordinator that merges and discards as necessary. This is terribly wasteful, because the coordinator would end up having to see all the sorted data, or at least the sorted keys of the data, compute the set of records that are actually on the window, and then fetch that.

Another simple approach that may be good enough for some cases is to have each shard generate a locally sorted list of elements from 0 to the maximum element position (k+pageSize).

For example, if we want the 100th through 102nd elements sorted over the full data (k=100, pageSize=2), each shard would build the sorted list of the first 102 elements in the shard.

The lists from each shard can be merged (in sort order) and only the first 102 elements retained.

When all lists from all shards have been merged, the elements in the 100th through 102nd positions represent the desired result.

Note that even if a shard does not have enough elements in its local list, the merged results from all the shards may have enough elements.

The problem with this approach is that while easy to implement, the further down you paginate into it (k becomes bigger), more data is needed to be shipped and merged. If you have a few hundred million records and you try to paginate about the middle of them it’s not pretty,

We can do better.

A distributed paginated sort

With more communication between the coordinator and the shards we can greatly reduce the amount of data that needs to be shipped around the network (at the cost of some latency due to additional round trips).

The general intuition for this algorithm is that the leftmost elements sent by each shard in the algorithm I just described (the not so simple one) are mostly redundant, and with some care we can avoid sending them to the coordinator.

This algorithm assumes each shard can hold its locally filtered and sorted set of keys without much trouble.

There are three stages to it, or round trips between the coordinator and the shards, where the coordinator helps the shards figure out which information is redundant.

We also introduce the notion of filtering the data before sorting, since it’s a common operation (think SELECT * FROM ... WHERE ... ORDER BY ...), applications don’t typically sort entired datasets.

Round trip 1

We first filter on each shard (we could also sort, but it’s not strictly necessary at this point) and return the number of elements that match the filter to the coordinator which adds them up for all shards.

This total across shards we will refer to as totalLen, and is the total number of elements in the filtered and sorted data. We need this to estimate where the window is on the global sorted data (if it existed in one place).

The insight is that k/totalLen is a number between 0 and 1 that can be used to approximate the beginning of the desired data in each shard if we assume data across shards is randomly distributed.

This step can be skipped if totalLen can be obtained in some other way.

Round trip 2

On each shard, we sort the filtered data and compute a local window. The sort could have happened in the previous round trip or while we returned the local length (so as to increase parallelism).

We’ll refer to the filtered sorted keys in the shard as data. Assume it’s an array or something that’s randomly accessible by a zero based index.

The local window is defined by two keys, a minimum key and a maximum key. We compute each key’s offset into the sorted data as follows:

• minKeyOff: max(0, (k * length(data)) / totalLen)
• maxKeyOff: min(minKeyOff + pageSize, length(data) - 1)

And return data[minKeyOff] and data[maxKeyOff]

The intuition here is that if we know the total length of the data, we can guess where our local window should be. But this is not enough information to paginate into the data, we need all local windows to be adjacent to each other without holes between them (i.e. missing elements). We’ll see why later.

Once all the local window edges are known, the coordinator merges them by picking the smallest data[minKeyOff] returned and the largest data[maxKeyOff].

We’ll call these minKey and maxKey. These two keys define a global window that should contain our page and we’ll use in the third round trip to ensure local windows are contiguous in the globally sorted data.

Round trip 3

Once again we go to each shard, but this time we send minKey and maxKey. Each shard expands its local window (as computed in round 2) to include all elements between minKey and maxKey.

This expansion ensures that between the slices of each shard there are no gaps where we could miss some element that would be present if we could hold all the data in one place.

Each shard then returns:

• nLeft: number of elements left of the corrected local window
• windowElements: all elements in the local window.

Once we’re on the coordinator, we add up all the nLeft values for each shard and merge all the windowElements (merge as merge sort uses the term), we’ll call this merged.

Then we can carve a page out of merged as follows:

copyOfRange(merged, 
k - nLeftSum, 
min(k - nLeftSum + pageSize, length(merged)))

If the data is well behaved, the data shipped is roughly proportional to the page size and the number of shards and doesn’t depend on how far we paginate nor on how much data we have (with the exception of a dataset with many duplicate keys).

Additional Notes

Why does this work?

The trick is in the interaction between the initial local window selection and the subsequent window expansion.

The local window start for each shard is chosen in round two as follows:

Where \(S_i\) is the ith shard’s data length (the floor is to account for using integer arithmetic). Note that local windows can sometimes be expanded. For the start value it means this initial value is an upper bound since expansion makes this number smaller.

We know by round one that \(totalLen\) is the sum of all shard’s lengths:

and \(nLeftSum\) is smaller than or equal to the sum of all window starts (due to the initial choice of window):

which we can simplify:

And use it as a bound for \(nLeftSum\):

The only case when \(nLeftSum\) is actually smaller than \(k\), is when some of the local windows were expanded to include additional elements, making merged larger to compensate in the same amount as \(nLeftSum\) is smaller.

Since each shard sends at least \(pageSize\) elements, the desired window is always contained in \(merged\) (with the exception of when \(k\) is close to the end of the sorted data).

This is easy to see with an example. Let’s say we have two similar shards after sorting and filtering, and we want the page with k=4, pageSize=3, the initial local window selection yields:

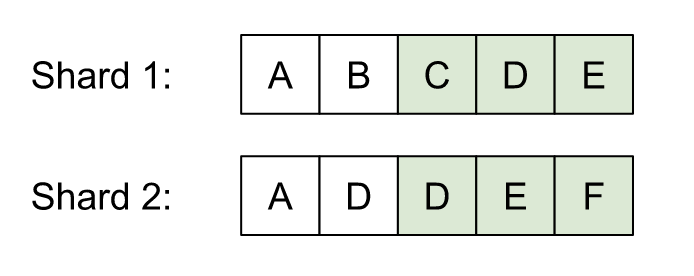
NOTE: Observe that in the example the data has 10 elements, but the desired offset k=4, so each local window starts after the second element. That is because when k=4 is scaled to the size of each shard’s local data, it’s roughly divided in half, since there are two shards

If these were the definitive windows, it’s nLeftSum would be 4 which is equal to k and merged would have 6 elements. But since we need to ensure one extra D is included in shard 2, we expand the windows to:

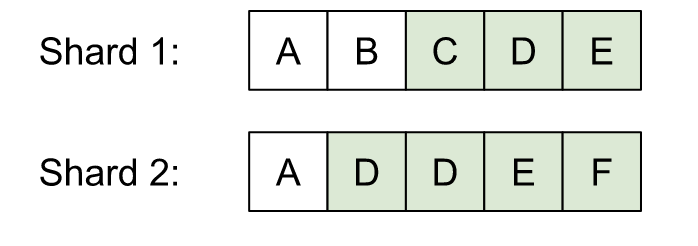
Now, nLeftSum is equal to 3, one less than k, but merged has been expanded by one element; the same amount which nLeftSum decreased. The merged set is always expanded to the left by k - nLeftSum and it typically holds at least nShards*pageSize elements (this doesn’t hold when we’re picking a window at the end of the sorted data).

The worst case for this algorithm in terms of transferred data is when the shards are fragments of a sorted set. Put another way, there’s some concatenation of the shards that yields the globally sorted data. For example, with k=6, pageSize=2 and three shards:

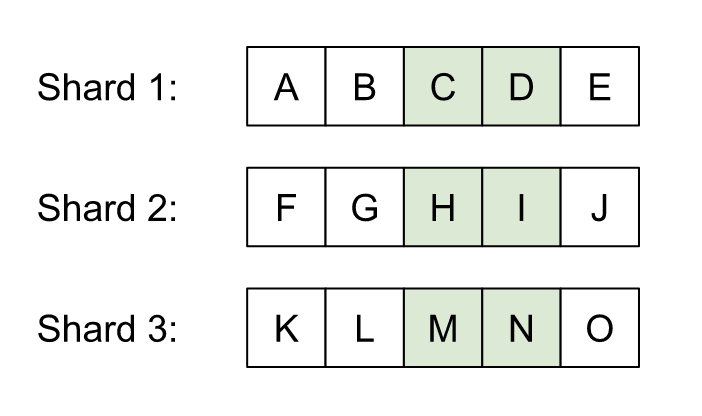
In this case, window expansion ensures any element larger than C and smaller than N has to be sent to the coordinator:

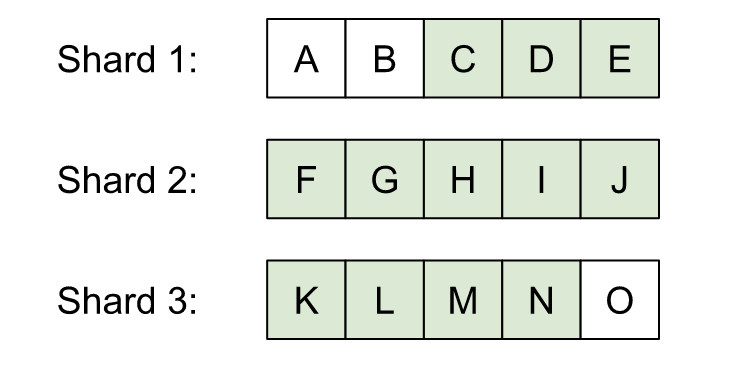
Essentially transferring most of the data to the coordinator.

On the other hand, if the shards are mostly randomly distributed, the amount of data shipped is on the order of nShards*pageSize.

Implementation

The following is a simple implementation of the basic concepts of the algorithm:

import static java.lang.Math.max;
import static java.lang.Math.min;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;

public class DistributedSort {
    /**
     * Window bounds
     *
     * @param <K> key type
     */
    static class Bounds<K extends Comparable<K>> {
        final K low;
        final K high;

        Bounds(K low, K high) {
            this.low = low;
            this.high = high;
        }
    }

    /**
     * The resulting local window
     *
     * @param <K> key type
     */
    static class LocalWindow<K extends Comparable<K>> {
        final int nLeft;
        final List<K> windowElements;

        LocalWindow(int nLeft, List<K> windowElements) {
            this.nLeft = nLeft;
            this.windowElements = windowElements;
        }
    }

    /**
     * State of a shard for a single sort operation
     *
     * @param <K> key type
     */
    static class Shard<K extends Comparable<K>> {
        final List<K> data;
        int minKeyOff = -1;
        int maxKeyOff = -1;

        Shard(List<K> data) {
            this.data = data;
        }

        int sortAndFilter() {
            // We just sort the shard's data
            data.sort(Comparator.naturalOrder());
            return data.size();
        }

        Bounds<K> getLocalWindowBounds(int k, int pageSize, int totalLen) {
            minKeyOff = max(0, (k * data.size()) / totalLen);
            maxKeyOff = min(minKeyOff + pageSize, data.size() - 1);
            return new Bounds<>(data.get(minKeyOff), data.get(maxKeyOff));
        }

        public LocalWindow<K> getResult(K minKey, K maxKey) {
            // Expand local window to the left
            while (minKeyOff > 0 && data.get(minKeyOff - 1).compareTo(minKey) >= 0) {
                --minKeyOff;
            }
            // Expand local window to the right
            while (maxKeyOff + 1 < data.size() && data.get(maxKeyOff + 1).compareTo(maxKey) <= 0) {
                ++maxKeyOff;
            }
            return new LocalWindow<>(minKeyOff, copyOfRange(data, minKeyOff, maxKeyOff + 1));
        }
    }

    /**
     * The coordinator's state for a single sort operation
     *
     * @param <K> key type
     */
    static class Coordinator<K extends Comparable<K>> {
        final List<Shard<K>> shards;

        Coordinator(List<Shard<K>> shards) {
            this.shards = shards;
        }

        /**
         * Sort entry point. This method simulates the communication with the shards.
         * It does not introduce parallelism for clarity, calls in each round can be issued
         * in parallel, only synchronizing when processing results.
         *
         * @param k        start offset
         * @param pageSize desired page size
         * @return the sorted page
         */
        List<K> sortedPage(int k, int pageSize) {
            // Round one, how much data is there, trigger the sort
            final int totalLen = shards.stream()
                    .mapToInt(Shard::sortAndFilter)
                    .sum();

            // Round two, find global window bounds
            K minKey = null, maxKey = null;
            for (Shard<K> shard : shards) {
                final Bounds<K> localWindow = shard.getLocalWindowBounds(k, pageSize, totalLen);
                if (minKey == null || localWindow.low.compareTo(minKey) < 0) {
                    minKey = localWindow.low;
                }
                if (maxKey == null || localWindow.high.compareTo(maxKey) > 0) {
                    maxKey = localWindow.high;
                }
            }

            // Round three, merge results
            final List<K> merged = new ArrayList<>();
            int nLeftSum = 0;
            for (Shard<K> shard : shards) {
                LocalWindow<K> localWindow = shard.getResult(minKey, maxKey);
                nLeftSum += localWindow.nLeft;
                // We'll do a simple add and sort for simplicity,
                // a mergeSort style merge would be better
                merged.addAll(localWindow.windowElements);
            }
            merged.sort(Comparator.naturalOrder());

            return copyOfRange(merged,
                    k - nLeftSum,
                    min(k - nLeftSum + pageSize, merged.size()));
        }
    }

    private static <K> List<K> copyOfRange(List<K> list, int fromInclusive, int toExclusive) {
        return new ArrayList<>(list.subList(fromInclusive, toExclusive));
    }

    public static void main(String[] args) {
        Coordinator<String> c;
        List<String> page;

        // Example 1
        c = new Coordinator<>(List.of(
                new Shard<>(new ArrayList<>(List.of("A", "B", "C", "D", "E"))),
                new Shard<>(new ArrayList<>(List.of("A", "D", "D", "E", "F")))
        ));

        page = c.sortedPage(4, 3);
        System.out.println("Example 1: " + page);

        // Example 2
        c = new Coordinator<>(List.of(
                new Shard<>(new ArrayList<>(List.of("A", "B", "C", "D", "E"))),
                new Shard<>(new ArrayList<>(List.of("F", "G", "H", "I", "J"))),
                new Shard<>(new ArrayList<>(List.of("K", "L", "M", "N", "O")))
        ));

        page = c.sortedPage(6, 2);
        System.out.println("Example 2: " + page);
    }
}